
i 번째 Energy level 에서의 양자 상태 수를 qi, 전자의 수를 Ni 라고 가정한다. 파울리 베타 원리에 의해, 하나의 양자 상태에는 최대 하나의 전자만이 허용될 수 있다. Ni ≤ qi 의 조건으로, i 번째 Energy level 에서 Ni 의 입자들을 qi 에 배열하는 경우의 수는 다음과 같다.

하지만, 각각의 입자(전자)들은 서로 구분이 불가능하므로, 경우의 수 계산에 포함하지 않는다. 따라서, i 번째 Energy level 에서 Ni 입자의 분포를 나타내는 실제 독립적인 경우의 수는 다음과 같다.

i 번째를 포함한 전체 경우의 수는, 첫 번째부터 i 번째까지의 모든 분포의 곱으로 나타낼 수 있다.

위 식으로부터 존재할 가능성이 가장 높은 입자의 분포를 구하면 된다. 즉, W 의 최댓값을 구하면 된다. W 의 최댓값은 분포를 변화시키는 에너지 레벨 중 Ni 를 변화시킴으로써 찾을 수 있지만, 동시에 총 입자 수와 총 에너지는 유지될 것이다.
이후, 양변에 log 를 취하고, 스털링 근사(Stirling's approximation)와 라그랑주 승수법(Lagrange multiplier)을 적용하여 다음과 같은 결과 식을 얻을 수 있다.

N(E) 는 단위 에너지의 단위 부피당 입자 수를 나타내고, g(E) 는 단위 에너지의 단위 부피당 양자 상태 수를 나타낸다. 함수 fF(E) 는 페르미-디락 분포(Fermi-Dirac distribution) 혹은 확률 함수라고 부르고, 에너지 E 에서의 양자 상태가 전자에 의해 사용 중인지에 대한 확률을 제시한다. 에너지 EF 는 페르미 에너지(Fermi Energy)라고 부른다. 또 다른 해석으로는 분포 함수 fF(E) 가 에너지 E 에서 채워진 양자 상태의 전체에 대한 비율을 나타낸다는 것이다.
The Distribution Function and the Fermi Energy.


T = 0K 에서 E < EF 인 경우를 생각해보면, 지수 부분은 exp( - ∞) = 0 이다. 따라서, fF(E) = 1 이다. 반대로, T = 0K 에서 E > EF 인 경우를 생각해보면, 지수 부분은 exp( + ∞) = ∞ 이다. 따라서, fF(E) = 0 이다. 이러한 결과는, T = 0K 에서 전자들은 그들이 존재할 수 있는 가장 낮은 에너지 상태에 존재한다는 것을 보여준다.
E < EF 에서 양자 상태가 사용 중일 확률은 1 이고, E > EF 에서 양자 상태가 사용 중일 확률은 0 이다. T = 0K 에서 모든 전자들이 Fermi energy 보다 낮은 에너지를 가진다는 것을 알 수 있다.

전자들은 가능한 가장 낮은 에너지 상태를 가지려 하기 때문에, 13 개의 전자를 가진 위 시스템의 양자 상태는 E1 부터 E4 까지 채워질 확률이 100% 라고 할 수 있다. 또한, T = 0K 에서 입자의 Fermi energy level 은 E4 와 E5 사이에 존재함을 예측할 수 있다.

이제 양자 상태의 밀도, g(E) 가 위 그림처럼 연속적인 에너지 함수의 형태라고 생각해보자. 만약 이 시스템 N0 의 전자를 가지고 있다면, T = 0K 에서 양자 상태 사이의 전자들의 분포는 점선으로 표시된다. 동일하게, 전자들은 가능한 가장 낮은 에너지 상태에 있으려 하기 때문에, EF 아래의 상태는 모두 채워져 있고, EF 위의 상태는 모두 비워져 있게 된다.
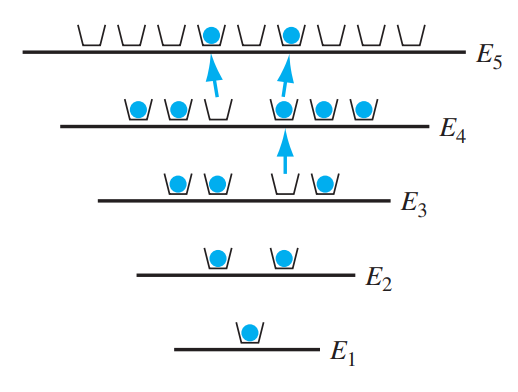
온도가 T = 0K 이상으로 올라간다면 어떻게 될까? 전자들은 열적 에너지(Thermal Energy)를 얻어 더 높은 Energy level 로 올라가게 되고, 이는 가능한 에너지 상태의 전자들의 분포가 변한다는 것을 의미한다. 위 그림은 T = 0K 의 양자 상태의 전자들의 분포가 변했음을 보여준다. E4 로부터 2 개의 전자가 충분한 에너지를 얻어 E5 로 이동했고, E3 의 전자 하나가 E4 로 이동했다. 온도가 변함에 따라, 전자의 분포 대 에너지가 변화한다는 것이다.
이러한 T > 0K 에서의 전자 분포 변화는 페르미-디락 분포 함수를 통해 관찰할 수 있다. 만약 E = EF 이고, T >0K 라면 fF(E) 함수는 다음과 같이 변하게 된다.
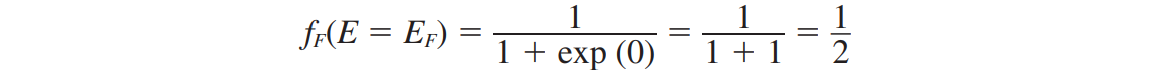
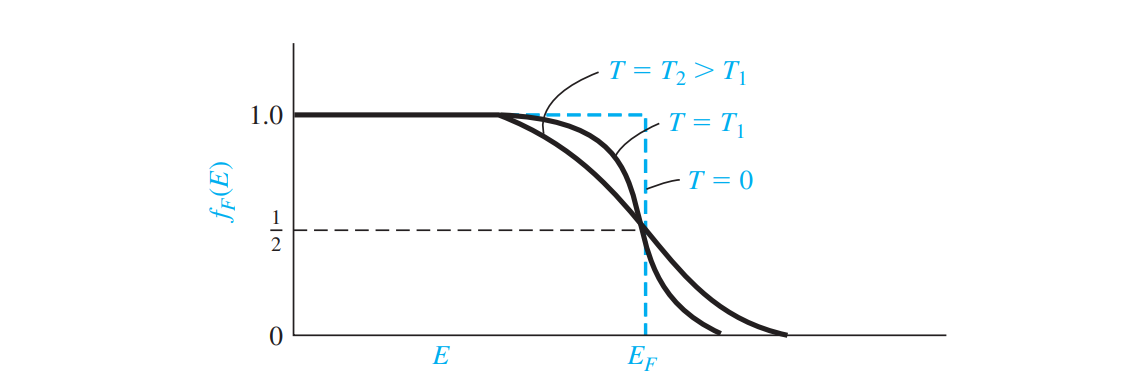
E = EF 에서 양자 상태가 채워져 있을 확률은 1/2 이다. 따라서, 페르미 에너지 EF 는 전자가 존재할 확률이 1/2 일 때, 전자가 가지는 에너지 준위를 의미한다. 아래 그림은 온도에 따른 페르미-디락 분포 함수를 보여주고, 페르미 에너지가 온도에 대해서 독립적이라는 것을 나타낸다. 이러한 결과는 전자들의 열적 에너지가 증가와 함께 더 높은 에너지 레벨로 이동한다는 것을 다시 한 번 보여준다.
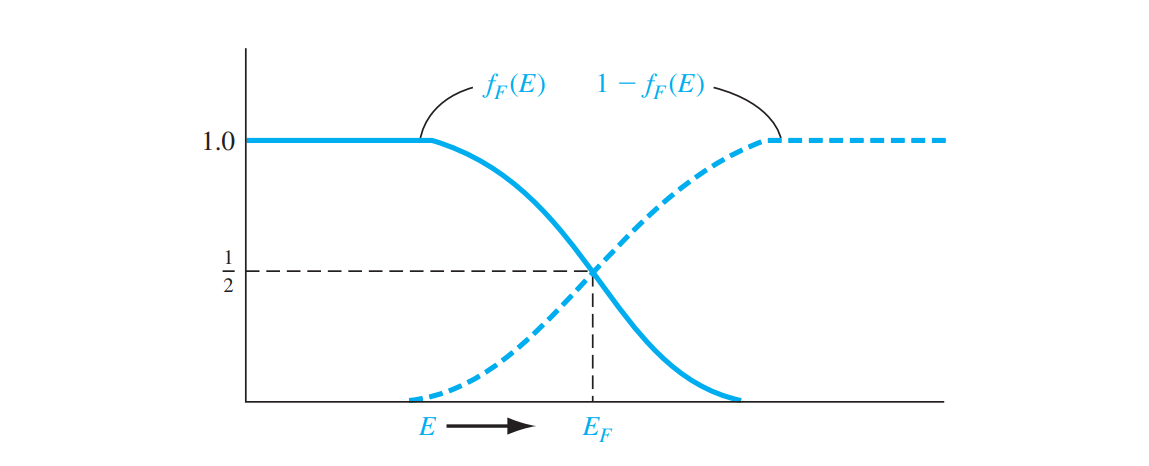
여기서, EF 에서 왼쪽으로 dE 의 거리만큼 떨어져 채워진(occupied) 상태의 확률과 오른쪽으로 dE 의 거리만큼 떨어져 비어(empty) 있는 상태의 확률은 서로 같다는 것을 알 수 있다. 페르미 에너지 EF 를 기준으로, fF(E) 와 1 - fF(E) 함수는 대칭이라는 것 또한 알 수 있다.
E - EF >> kT 의 경우, fF(E) 함수에서 지수 항이 가장 지배적이게 되므로, 나머지 항을 무시할 수 있게 되며 페르미-디락 분포 함수는 다음과 같이 변형 가능하다.
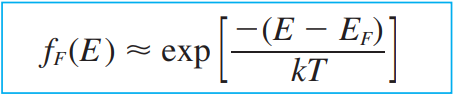
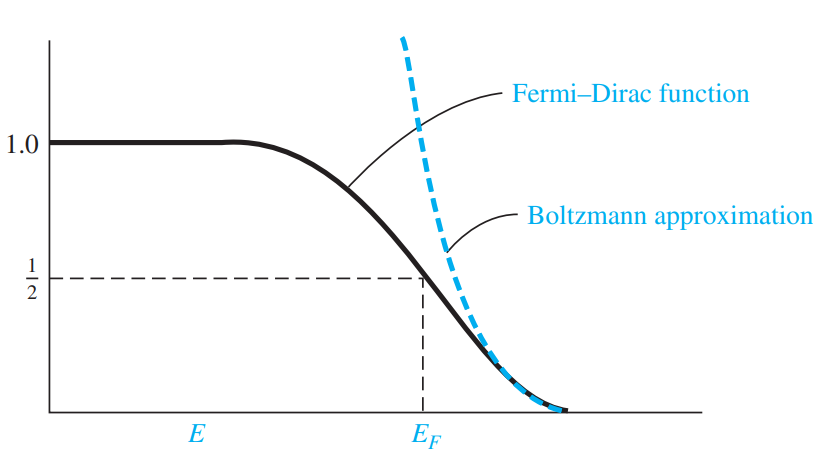
이는 Fermi-Dirac distribution function 에 대한 Maxwell-Boltzmann approximation 이다. 아래는 Fermi-Dirac probability function 과 Boltzmann approximation 을 나타낸 그림이며, approximation 에 대한 유효한 에너지 값의 범위를 제공한다.
'전공 > 물리전자공학' 카테고리의 다른 글
| The Intrinsic Carrier Concentration. (0) | 2023.07.03 |
|---|---|
| Charge Carriers In Semiconductors. [n0, p0] (0) | 2023.06.28 |
| Formation of Energy Bands (0) | 2023.06.26 |


